¿Cuántas personas harían falta para que dos de ellas cumpliesen años el mismo día?
Realmente esta no es una paradoja real ya que el problema surge al guiarnos por la intuición. Pero realmente no contradice a la lógica en ningún momento. De hecho es bastante sencillo de comprender una vez se explica detenidamente.
Pongamos un escenario ficticio. Hay una fiesta de cumpleaños a la que asisten 365 personas, que van llegando de una en una. ¿Cuantas harían falta para que la probabilidad sea próxima al resultado que queremos obtener? Los resultados son sorprendentes ya que, teniendo en cuenta que hay 365 días posibles, sólo harían falta 23 personas para que la probabilidad de que dos de ellas coincidan en cumpleaños sea de un 50%. Y para conseguir un 99% de probabilidades necesitariamos a 57. Pero, ¿a qué son debidos estos números tan pequeños? Son debidos en realidad al erroneo acercamiento al problema. Pero primero, repasemos algo de teoria básica de clase.
Según Laplace, la probabilidad de que algo suceda P(A) es el resultado de casos favorables entre casos posibles:
La probabilidad de que algo no suceda es 1 menos la probabilidad de que suceda:
Y por último, la probabilidad de que ocurran dos sucesos es la probabilidad de uno por la del otro:
Teniendo esto en cuenta, analicemos el problema:
Vamos a proceder a calcular, no la probabilidad inicial, si no la probabilidad de que en la fiesta no haya nadie que cumpla años el mismo día. Para ello vamos a tener en cuenta lo siguiente:
Los casos posibles van a ser en todo momento 365 (días del año). Y los casos favorables serán: si hay dos personas, 365 - 1; en caso de haber 3 personas, 365 - 2; en caso de haber n personas, 365 - (n - 1) (las personas que ya han ocupado una fecha de cumpleaños).
Si calculamos las probabilidades de que el primer planteamiento del problema suceda, utilizando la ecuación de 1 - la ecuación que acabamos de calcular, obtenemos esta gráfica.
Vemos así los sorprendentes y poco intuitivos resultados de este problema.
Como conclusión podemos decir que la probabilidad puede darnos resultados que no esperabamos en un principio y que debemos hacer cálculos antes de llegar a conclusiónes que parecen obvias de forma precipitada.
Fuentes:
https://en.wikipedia.org/wiki/Birthday_problem
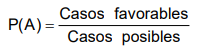



No hay comentarios:
Publicar un comentario